'Mathematics reveals its secrets only to those who approach it with pure love, for its own beauty'

Archimedes 

At St Joseph’s, we believe that every child can experience success and enjoy Mathematics regardless of their background. We believe that mathematical ability is not innate, it is increased through effort. Through our Mathematics curriculum, we aim to develop a culture of deep understanding, confidence and competence in Mathematics which will in turn, produce strong, secure learning and real progress.  Mathematics is integral to all aspects of life. Because of this, we strive to ensure that our pupils develop a positive and enthusiastic attitude towards Mathematics and that through our Mathematics teaching, our pupils become fluent, confident and independent mathematicians that will stay with them as they become lifelong learners.

Through the teaching of mathematics, our aims are: 

• Success for all - Every pupil can enjoy and succeed in mathematics. A growth mindset enables pupils to develop resilience and confidence. 
• Deeper understanding - Pupils must be given time and opportunities to fully explore mathematical concepts. The challenge comes from investigating ideas in new and complex ways. 
• Problem-solving - Enabling pupils to solve new problems in unfamiliar contexts is the ultimate aim of our mathematics education. Identifying, applying and connecting ideas enables pupils to tackle new and more complex problems.
• Mathematical thinking - Successful mathematicians are known to develop mathematical ‘habits of mind’. To encourage this, we support pupils to be systematic, generalise and seek out patterns. 
• Mathematical language - Mathematical language strengthens conceptual understanding by enabling pupils to explain and reason. 
• Multiple representations - Objects, pictures, numbers and symbols enable pupils to represent ideas and make connections in different ways. This develops understanding and problem solving skills – while making lessons engaging and fun. 

Curriculum Intent for Mathematics

Curriculum Implementation for Mathematics

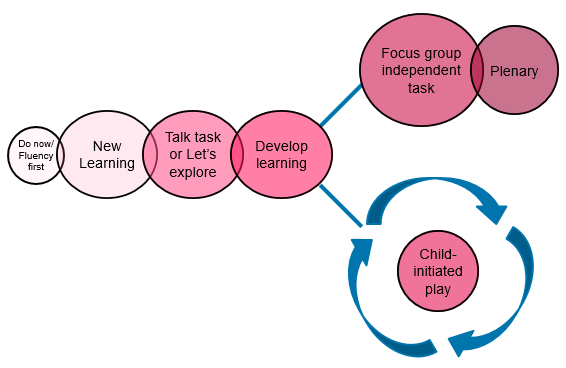
The six-part lesson for Mathematics

The Mathematics Mastery six-part lesson structure is unique and allows teachers to take control of the learning, based on what is happening in the classroom that day. Assessment for learning opportunities are threaded throughout, constantly building upon what pupils are learning at every stage in the lesson.

Throughout the lesson, teachers will have high expectations of vocabulary and talk. Pupils are expected to use the correct vocabulary, talking and answering in full sentences at all times.

Transitions: Pupils in EYFS and KS1 will use transitions to move between different parts of the lesson and tasks from the carpet to the tables. These will include singing and chanting to recall key number facts.

1. Do now: Pupils review and practise previous knowledge learned.
2. New learning: The Key Learning and key vocabulary (known as star words) are shared and rehearsed. The teacher (and pupils) model using concrete manipulatives. Misconceptions are anticipated and incorporated. The Talk task/Let’s Explore task is modelled.
3. Talk task/Let’s Explore: Pupils have the opportunity to practise key vocabulary and the learning taught so far. Everyone is expected to talk in full sentences, using words and symbols accurately, manipulating objects when appropriate.
4. Develop learning: References are made to previously learnt models/representations/skills/concepts. The Key Learning is further developed using words and symbols accurately through accurate modelling. The Independent Learning task is modelled. Misconceptions are anticipated and incorporated.
5. Independent Learning: Pupils complete the task with access to appropriate concrete manipulatives. There is an emphasis on understanding and developing fluency with extension tasks involving deeper understanding of the same mathematical concept or skill - through solving less routine problems, demonstrating using concrete manipulatives/ drawing diagrams, explaining in full sentences or asking their own questions
6. Plenary:  Pupils will have the chance to reflect on their learning that day discussing their lesson question or celebrating their work.

In EYFS, teachers adopt a similar approach using the focus group model below:

Adaptations

The majority of pupils in a class move through the programme of study at broadly the same pace and are exposed to the same questions during lessons. Pupils in all classes sit in mixed ability pairings during all or part of the lesson to allow collaborative learning, exposure to different opinions about the same work and regular opportunities for discussion of answers to support pupils’ reasoning skills and check and deepen their understanding. Pupils are supported by the structure of the lesson, their peers and additional adults as well as scaffolds provided by teachers. Pupils are extended as a result of higher order questioning where conjectures and generalisations are required. It is expected that all pupils will experience challenge in a lesson through exposure to rich problem solving tasks and pattern spotting, rather than acceleration to new content.

Depth Symbols

In order for pupils to develop as active mathematicians, we need to provide opportunities for them to ask questions and create their own problems to explore. This is a great way to develop deep understanding but it also fosters curiosity and creativity in mathematics. We use ten ideas that challenge pupils to develop a depth of understanding within a concept, rather than moving them on to a new objective. Each of the ten ideas is represented by a picture or symbol. The idea being that, after introduction, the tasks can be easily identified by pupils without the need for instruction. Depth tasks are incorporated in every lesson.

• Misconception: Can you explain what is wrong with this and correct the error?
• What’s the same? What’s different? Can you find anything that is the same about these two numbers/shapes/calculations? Now can you find something that is different?
• Spot the odd one out: Find an odd one out and explain why it doesn’t fit. Does your partner agree with you? Could another one be the odd one out? Why? Can you give another example that would be an ‘odd one out’ in this set?
• Explain it! Explain to your partner how you know. Remember to use our star words.
• What’s the question? If this is the answer, what could the question have been? This provides opportunities for pupils to think of multiple appropriate equations or word problems for the given ‘answer’. Pupils can also be challenged to think of non-examples, e.g. what could the question not have been?
• Maths story: Make up a real-life story using your equation, numbers or shapes. Try to use the star words
• All possibilities: Is there more than one way of completing this? Is there more than one answer? Have you found them all? Can you prove that?
• Draw it! Draw a picture to explain or demonstrate what you have worked out. This could include pictorial representation or concrete manipulatives, or other informal sketches.
• Show me: Convince me that you are right using concrete manipulatives. The ability to show the same concept using different manipulatives and explain the similarities and differences between representations and demonstrates a greater depth of understanding.
• Find a pattern: Can you see a pattern (in the numbers)? Can you see a pattern in the answers? Continuing this pattern, what would happen if …? What came before? What comes next? Explain how you know.

 The importance of vocabulary and modelling

‘A child cannot pursue mastery of a mathematics topic without understanding the vocabulary associated with it. It is this vocabulary that truly enables children to engage with concepts and build a deep understanding of them.’ (Eliot Morgan, Third Space Learning)

Correct vocabulary is used from Reception class onwards and is shared at the beginning of each lesson. There is also the expectation that they use this correct vocabulary throughout e.g. equation not number sentence, is equal to not equals. Pupils are also expected to answer in full sentences throughout the lesson. In EYFS and Key Stage 1, this may be through the use of ‘My turn, your turn’ to model the clear sentence structures to support their early communication skills. In Key Stage 2 the vocabulary is shared and recapped at the start of each lesson, where definitions of key-words are learnt and put into context.

To find out what vocabulary your child will be learning, please see the document below:

VOCABULARY LIST

Linked to the principle of Conceptual Understanding, each lesson includes modelling by the teacher. Teachers use the Concrete, Pictorial and Abstract approach and will choose which one (or more than one) to use within the lesson. During the ‘Talk task/Let’s Explore’ part of the lesson, pupils have a go at using the correct vocabulary and modelling with their partners to further embed the knowledge taught.

To find out what representations your child will be learning, please see the document below:

KEY REPRESENTATIONS DOCUMENT

Maths Meetings

Daily sessions are timetabled for all years and are used to consolidate key areas of maths based on assessment and curriculum coverage. Maths meetings provide an opportunity for children to revisit key concepts throughout the year and increase their memorisation of key facts that may not be explicitly covered during all maths lessons. This means that as pupils are practising concepts and skills on a regular basis; they continually build on their mastery of these concepts and are more likely to become fluent.

Arithmetic Skills

To aid in the progression of Maths, in Year 5 and 6, Arithmetic Skills lessons have been introduced. These lessons are taught 3/4 times a week, where a weekly assessment takes place on a Friday. Each week a new concept or skill is taught explicitly to the children, where they practice that skill in the lessons and common misconceptions are addressed throughout the week. The children will then sit an assessment that is non-progressive (allowing improvements in scores to show progression in knowledge) and covers all arithmetic areas for that year group. This will ensure that even after a skill has been taught it is being practised and used at least once a week. Throughout the academic year each concept or skill will be revisited more than once, to allow misconceptions to be taught again.

Same Day Intervention

A small number of pupils receive additional support (by the class teacher where possible) following the lesson. This ensures no child falls behind because of a lack of conceptual understanding. If more pupils require support, then the lesson is retaught the following day using variation to focus on the areas of misconception.

Assessment in Mathematics

Teachers use Assessment for Learning throughout their lessons through questioning. During the ‘Talk task/Let’s explore task’, adults will listen for pupils using the correct vocabulary and using the manipulatives correctly to spot and highlight any misconceptions within the lesson. Teachers will formatively assess pupils against the Key Learning using pupils’ Key Learning stickers. If a pupil has met the Key Learning, the teacher will highlight the Key Learning with green. If a pupil is working towards the Key Learning, the teacher will highlight the Key Learning with orange and green. If a pupil needs further work against the Key Learning, the teacher will highlight the Key Learning orange and there will be evidence of an intervention before the next lesson. Teachers will also note on the Key Learning whether the pupil has had teacher/teaching assistant support to inform formative assessment.  Summative maths assessments are completed throughout the year to evidence how pupils have independently applied the maths’ skills taught. Teachers use this information to make judgements about progress and attainment which is inputted into the school’s assessment system. Senior Leaders as well as the Mathematics leader analyse this data to ensure good progress from all groups of learners is made as well as spotting any patterns between different groups. This information is then shared with all teachers in school.

Our Calculation Policy

As a Mathematics Mastery school, we adopt the Mathematics Mastery’s Calculation policy. To view our calculation policy, please click on the document below:

CALCULATION POLICY

Curriculum Impact for Mathematics

Through an inspiring and engaging mathematics curriculum, mathematics at St Joseph’s is viewed as an exciting and enjoyable subject where everyone can succeed. They know that it is reasonable to make mistakes because this can strengthen their learning through the journey to finding an answer. Pupils are confident to ‘have a go’ and choose the manipulatives they need to help them to learn along with the strategies they think are best suited to each problem. Pupils at St Josephs understand the relevance and importance of what they are learning in relation to real world concepts. They know that maths is a vital life skill that they will rely on now and in the future in many areas of their daily lives.

The impact of our Mathematics curriculum at St Joseph’s is monitored in various ways. Pupils’ progress across the curriculum is monitored at key points throughout the year to ensure progress is made towards National Curriculum objectives as well as the progress of targeted intervention groups.  Clear progression in year groups, key stages and across school is evident when looking at pupils' books.